Algorithmic worlds

Search blog posts

Next posts

2009-06-04 Piling hexagons

2009-05-02 Voronoi patterns

Blog

A blog about algorithmic art and fractal aesthetic. Click here to subscribe to the RSS feed.

May 2nd 2009

Another fast algorithm for Voronoi patterns

Voronoi patterns are drawn in the following way. Pick points randomly in the plane. Then color each pixel according to its distance to the closest among the chosen points. You get something like this :

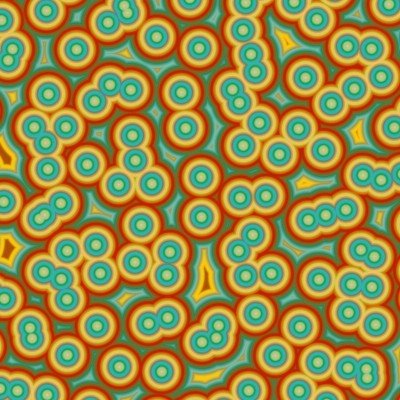
or like this

if you use a slightly more elaborate function of the distance.

The trouble is that such an algorithm is not efficiently implemented in Ultra Fractal. The latter computes pixel by pixel : the same algorithm is repeated for each pixel, only the input consisting of the pixel coordinates change. Therefore with a naive algorithm, for each pixel, one has to compute the distances to all of the points (to find the closest one) which requires a huge amount of computations.

One possible improvement is to avoid picking points completely randomly. If one chooses each of them randomly in a region centered on a vertex of a regular gird, then, given a pixel, it is possible to find the closed point by computing only a very small number of distances. This improves the speed of the algorithm spectacularly. Moreover, by tuning the maximal distance from a point to the corresponding vertex of the gird, one can interpolate between a completely regular gird and something close to a true Voronoi pattern, what can be interesting artistically. For instance the image below, while still retaining some randomness, is much closer to a regular square tiling than the image above. The trouble with this kind of algorithms is that the patterns they produce are necessarily too regular, compared to a genuine Voronoi tiling.

There is a third algorithm which seems to work pretty well. Simply choose the random points as the vertice of regular girds which are randomly scaled and rotated. It is very easy to test the distance of a pixel to the vertice of a gird, so this algorithm is quite fast. If all the girds are large enough and if there are sufficiently many of them, the result is pretty close (at least to the eye) to a true Voronoi pattern, and does not suffer the lack of randomness of the previous algorithm.

Finally, here is an image made with this algorithm. The leaf shapes which are apparently randomly distributed are actually on the vertice of square girds. The basic pattern was summed at various scales to produce an interesting image and give it a fractal flavour.