Algorithmic worlds

Search blog posts

Next posts

2012-03-30 Periodic Julia patterns

2012-03-25 Conformally invariant patt...

2012-03-21 In Flight

2012-03-16 Spherical worlds

2012-03-02 Ferrofluids

2012-02-26 Starry Night

2012-02-12 The Scale of the Universe

2012-01-17 Internet strike

2012-01-01 Gravity Stools

2011-11-01 Two animations

Previous posts

Blog

A blog about algorithmic art and fractal aesthetic. Subscribe to the RSS feed.

March 25th 2012

Conformally invariant patterns

In this post I'd like to elaborate a bit on the dense Julia sets that were the subject of a recent blog post. With some pictures, I'll illustrate the beautiful conformal invariance that these patterns enjoy. If you're not a math buff, don't get deterred by the slightly technical language at some points. Just enjoy the pictures, which should be rather self-explanatory.

Recall that a conformal transformation is a geometric transformation that preserves angles (check the Wikipedia page linked above for illustrations of this fact). Locally, a conformal transformation always look like a rescaling, combined with a translation and a rotation.

The sphere admits a large number of conformal transformations. In fact, if we picture it, like in the previous blog post, as the complex plane plus a point at infinity, any rational function (i.e. any ratio of two holomorphic polynomials) corresponds to a conformal transformation of the sphere. The dense Julia patterns that we considered were constructed by iterating this type conformal map, and it turns out that they inherit some very nice properties of conformal invariance. I do not know how to formulate these properties in a mathematically precise way, but I will illustrate them here with some pictures. I will compare the dense Julia pattern appearing in 20110808-1 with the "fractal Mondrian" pattern. Both patterns display dense fractal structures, but it will be obvious that the second one is not conformally invariant.

The two dense fractal pattern that we will compare.

Let us start with the stereographic map, which maps the plane plus a point at infinity to the sphere. This is an example of a conformal map. In the recent blog post, I told you that the dense Julia patterns can be mapped nicely and seamlessly on the sphere using this map. Indeed, here is what happens with the pattern of 20110808-1:

This is a view from "inside" the sphere on which the Julia pattern lives. To get "outside views" of spherical Julia sets, check Syntopia's recent blog post. Now here is what happens if we map the fractal Mondrian pattern on the sphere:

Observe how the pattern tends to accumulate near the south pole. This is due to the fact that the stereographic projection maps only a unit disk on the north hemisphere of the sphere and the rest of the plane on the south hemisphere. (It is a stereographic projection with respect to the south pole...) As the fractal Mondrian pattern is approximately translation invariant, it necessarily accumulates on the south hemisphere.

The next map is the squaring map z -> z². This is a 2 to 1 conformal map which produces an order 2 cyclic symmetry (a symmetry under rotation by 180°). Here it is applied to our two patterns:

The squaring transformation applied to our two patterns.

Again, remark how the dense Julia pattern looks "natural" or undeformed, while the fractal Mondrian pattern is clearly distorted. It is possible to repeat the experience for any power. Here are our patterns for the cubic map z -> z³, generating an order 3 cyclic symmetry (symmetry under rotations by 120°):

The cubic transformation applied to our two patterns.

Finally, we can use the fact that any holomorphic function generates a conformal transformation. Here is what happens to our pattern using a sine function:

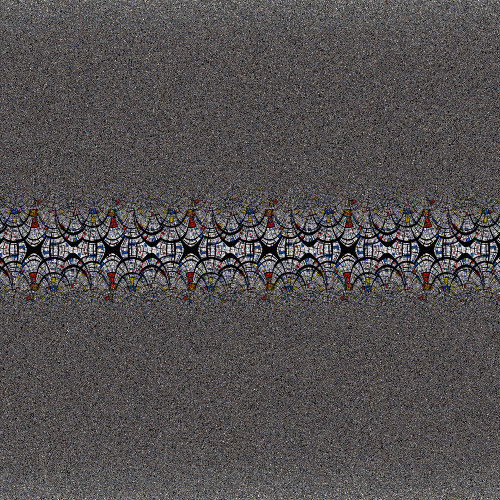
The sine transformation applied to our two patterns.

Again, the dense Julia pattern takes it very nicely, unlike the fractal Mondrian pattern. (The large gray areas are regions where the fractal Mondrian pattern is too small to be resolved.) Remark that for this choice of conformal map, the pattern becomes periodic in one direction (the real axis). Now here is a question: is there a conformal map that would allow to get periodicity in both directions? It would certainly be cool to have periodic Julia patterns! The answer is yes, and it has a suprising and nice geometrical interpretation, but this will be for the next blog post.